The $1,000,000 question about P vs NP which still remains unsolved
There is a $1,000,000 prize on offer for the first person to come up with a complete solution to the problem P versus NP. At its heart is the question “are there problems for which the answers can be checked by computers, but not found in a reasonable time?” If the answer to that is yes, then P does not equal NP. However, if all answers can be found easily as well as checked, if only we knew how, then P equals NP.
The P versus NP problem is a major unsolved problem in computer science. Informally, it asks whether every problem whose solution can be quickly verified by a computer can also be quickly solved by a computer.
It was essentially first mentioned in a 1956 letter written by Kurt Gödel to John von Neumann. Gödel asked whether a certain NP-complete problem could be solved in quadratic or linear time. The precise statement of the P versus NP problem was introduced in 1971 by Stephen Cook in his seminal paper “The complexity of theorem proving procedures” and is considered by many to be the most important open problem in the field. It is one of the seven Millennium Prize Problems selected by the Clay Mathematics Institute to carry a US$1,000,000 prize for the first correct solution.
The P vs NP is generally considered one of the most important open questions in mathematics and theoretical computer science as it has far-reaching consequences to other problems in mathematics, and to biology, philosophy and cryptography. If solved, it could open new doors for providing security to the Internet. ?Scott Aaronson from MIT states that,
“ If P = NP, then the world would be a profoundly different place than we usually assume it to be. There would be no special value in ‘creative leaps’, no fundamental gap between solving a problem and recognizing the solution once it’s found. “
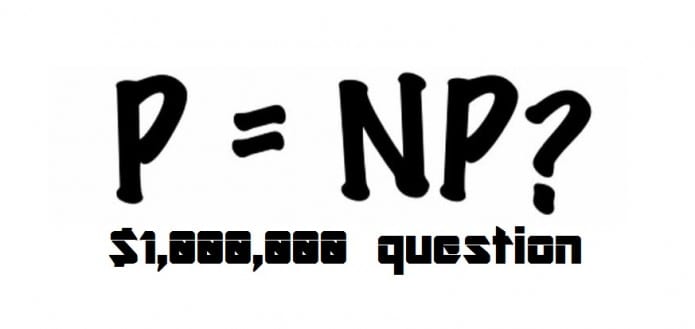
The p is a problem and the np is no problem so as far as I am concerned they cancel each other out so the problem solves it’s self because there was no problem to begin with .
hello guys, I know how to solve p vs np, it is very easy to solved. But I need to know is the money real or not.
If it is ,contact me soon.If it’s not then I well do not tell the answer.
the money is not real. what is the Ans to P vs NP